协方差(covariance )是一个统计量，是对一个样本的某一统计特性给出的一个估算量。
常见统计量
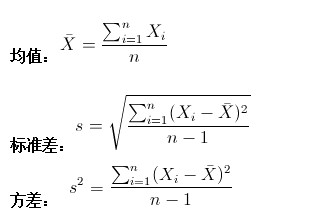
均值估算的是样本集合的平均水平。
方差估算的是样本集合的散布度，单元维度偏离其均值的程度。
那协方差(covariance)呢？
如果是一维样本不存在协方差(covariance)，
如果是二维（多维）样本呢？比如统计多个学科的考试成绩。
仿照方差的定义：
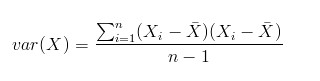
来度量各个维度偏离其均值的程度，协方差(covariance)可以这么来定义：
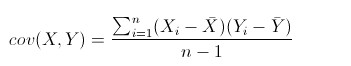
直觉理解一下就是：如果有X,Y两个变量，每个时刻(或点)的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积，再对这每时刻的乘积求和并求出均值（其实是求“期望”，但就不引申太多新概念了，简单认为就是求均值了）。
可以通俗的理解为：两个变量在变化过程中是同方向变化？还是反方向变化？同向或反向程度如何？你变大，同时我也变大，说明两个变量是同向变化正相关的，这时协方差就是正的。
从数值来看，协方差的数值越大，两个变量同向（正相关）程度也就越大。反之亦然。
variance和covariance的定义比较
还有一个就是协方差矩阵（Covariance matrix）
协方差矩阵是用于描述两个随机变量之间线性相关性的矩阵。
对两个随机变量X和Y,协方差矩阵定义为:
Cov(X, Y) = E[(X - E(X))(Y - E(Y))^T]
其中,E(X)和E(Y)分别表示X和Y的期望(均值)。
在概率论和统计学中，协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况
例如,对两个二维随机变量X和Y:
X = [x1, x2]
Y = [y1, y2]则其协方差矩阵为:
Cov(X, Y) =
[[Cov(x1, x1), Cov(x1, x2)],
[Cov(y1, x1), Cov(y1, x2)]]
可以看出对角线元素表示x1,x2和y1,y2各自的方差,非对角线元素表示x1与y1,x1与y2,x2与y1,x2与y2之间的协方差。
所以,协方差矩阵整体上表示两个随机变量在各维度上以及不同维度之间的相关性。
应用:协方差矩阵奇异值分解（SVD）
- 将X转置并与X相乘,等效于计算X和X在每个维度上对应坐标的内积。
- 内积反映了两个向量在某个维度上的相似程度,越相似内积越大。
- 因此$X_TX$的每个元素就是X和X在该维度上坐标的协方差
Σ是各主成分对数据方差的贡献，也就是各主成分的长度。它们不是权重，因为它们不一定加起来等于1。
奇异值分解可以看作是对矩阵S进行一个旋转、缩放和再旋转的操作，使得S变成一个对角矩阵³。这样可以提取出S的主要特征，例如方向、变化程度和线性相关性⁴。
应用：多维度高斯分布
多维高斯分布里面有两个参数，
一个是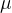
，可以用所以样本的均值来估计，代表总体数据的平均值。
一个是∑∑，就是前面的协方差矩阵，代表不同维度的相关联程度。
应用：PCA主成分析
本质上是找一个更低维度的表面（空间），使得投影到这个表面的数据与原数据之间的误差（距离）最小。
实现算法：
∑∑ is Sigma is 协方差矩阵，是nxn方阵 ，在经过了normalization之后求得的Sigma，本质上代表了数据集n个维度的相互关系。
在经过svd分解之后，我们主要用的是U，因为根据彻底理解SVD奇异值分解，我们知道U的列向量是 Col（ ∑∑ ）的一组标准正交基。
还有，U的列向量是从左到右，重要性逐步降低的，所以要降到k维，只需要取U的前k个列向量，这样就把原来n维的坐标系，降到了k维单位正交的坐标系。
而新的数据集的值则可以表示为：
