参考文章
-
为什么是“最小二乘”而不是“最小一乘”？
https://blog.csdn.net/fengzhuqiaoqiu/article/details/105226868
-
不借助sklearn的案例：
-
sklearn的案例：
-
梯度下降法讲解
-
线性回归公式推导及代码实现（非调包）
-
【机器学习】线性回归（超详细）
https://blog.csdn.net/weixin_51781852/article/details/122627291
关键概念
1.残差
残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话， 我们可以将残差看作误差的观测值。
在回归分析中，测定值与按回归方程预测的值之差，以δ表示。残差δ遵从正态分布N(0，σ2)。（δ-残差的均值）/残差的标准差，称为标准化残差，以δ表示。δ遵从标准正态分布N(0，1)。实验点的标准化残差落在(-2，2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2，2)区间以外，可在95%置信度将其判为异常实验点，不参与回归直线拟合。
显然，有多少对数据，就有多少个残差。残差分析就是通过残差所提供的信息，分析出数据的可靠性、周期性或其它干扰。残差计算即是残差的平方和除以(残差个数-1)的平方根。
2.最小二乘法
为什么是“最小二乘”而不是“最小一乘”？
其实很简单，“二乘”就是“平方”，在英文中这个位置的单词就是Squares。
该方法的基本原理有很好的解释了[1]。
总结成一句话来说就是：该方法通过最小误差的平方和寻找数据的最佳函数匹配。
以最简单的线性模型为例：
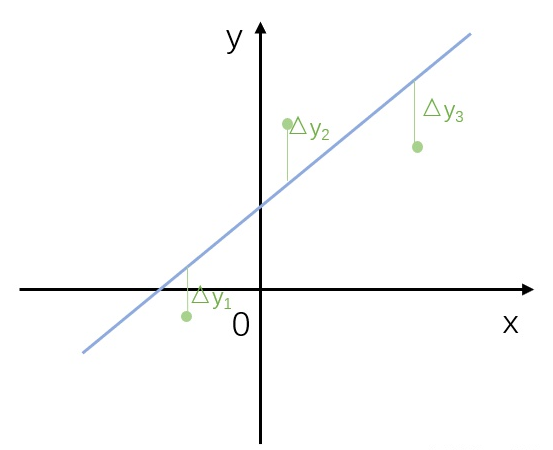
为什么是“最小二乘”？
（1）“最小一乘法”的解不一定唯一，举个例子：
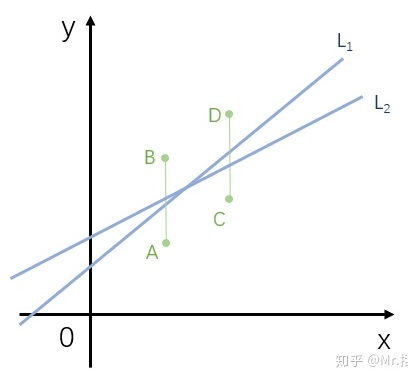
L1和L2都符合误差绝对值最小
使用最小一乘准则，可以构造出无数条样本回归直线，只要这些直线同时与AB、CD相交即可。
（2）方便求解
虽然在定义上最小一乘法更直观
但是在数学求解上最小二乘法要更简单，这点在线性回归上就有很明显的体现了。
（3）假定了误差服从正态分布的前提
还是对于线性分布的散点（假设有3个），他们相对理想的线性模型的误差可以写成：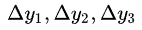 
。
我们假设这些误差服从正态分布。
为什么是正态分布？简单来说是因为他在生活中最常见。
回忆一下，标准正态分布的公式为：
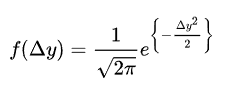
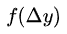就是观察到某散点与直线的误差为 
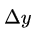概率。
根据极大似然估计的原理，三个数据点的联合概率就是：
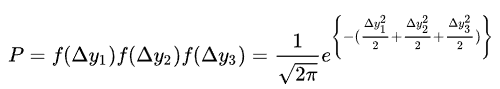
想让 P 的值最大，也就是让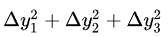 
的值最小。
这不就是最小二乘么？
所以说使用最小二乘法做线性回归是建立在残差为正态分布的假设上的。
那么如果假设残差不是正态分布，就不能用最小二乘了么？——是这样的。
最小二乘的短板
上边都是关于最小二乘的有点，但是他也有个明显的缺点：
当数据点中存在一个明显的离群值时，该影响会被最小二乘中的“平方”放大，对最终回归结果产生更大的影响。
3.学习率
梯度下降法的步长
4.代价函数
我们用假设函数来表示我们预测结果的模型。那么，这个模型好还是不好呢？我们需要有一个判别标准，这个标准就叫作代价函数。
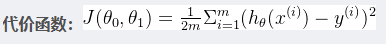
误差
预测值一定与真实值存在误差（用ε表示该误差）
对于每个样本：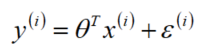
正太分布
- 独立同分布
正态分布公式：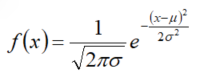
误差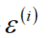
独立并且具有相同分布，并且服从均值为0，方差
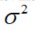的正态分布
独立：小明和小红的信用额度，彼此不影响
同分布：小明和小红都是在同一个银行正态分布：银行可能会多给一点，也可能会小给一点，但是浮动太大的概率会很小，符合正常状态
似然函数
什么样的参数和数据的组合后更接近真实值，让该组合接近真实值的概率越大越好，则需要似然函数数值越大越好
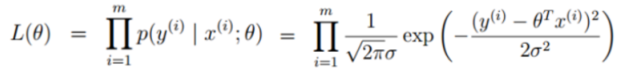
对数似然
将乘法运算转换成加法运算，就使用对数求和方法
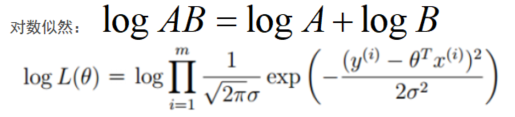
展开化简
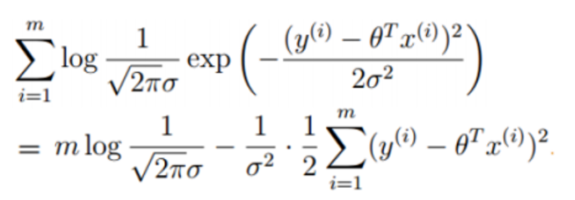
代价函数
让似然函数越大越好，则需要J(θ)越小越好。
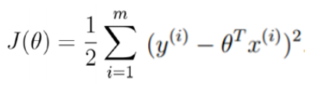
如果假设函数是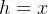
,那么易知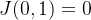
.通过对比这两个式子可知，当
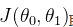取最小值时，误差最小，假设函数拟合的最好。
即我们的目的变成了，求当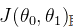
取最小值时，将其所对应的参数
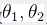，代入ℎ𝜃 (𝑥) = 𝜃0 + 𝜃1𝑥这个式子中即得假设函数。
如何求最小值？
- 最小二乘法
- 梯度下降法
- 牛顿法等
流程
-
加载数据集（数据清洗等）；
-
划分数据集，分出约25%的数据作为测试集；
sklearn的方法：
x_train, x_test, y_train, y_test_ori = train_test_split(feature, target, test_size=0.25) -
标准化或归一化；
-
建立线性回归模型；
-
通过最小二乘法或梯度下降法求得代价函数（参数）；
还有几种：随机梯度下降法、小批量梯度下降法、牛顿法、拟牛顿法等
-
测试集验证均方误差
from sklearn.metrics import mean_squared_error error = mean_squared_error(y_test_ori, y_predict_inverse)