数学定义
范数的公式是向量每个分量 绝对值 P 次方 求和, 再用幂函数计算 P 分之一,这里 P 肯定是整数
$$\sqrt{a^2+b^2}$$
(\sqrt{a^2+b^2})
1,2,3...到正无穷都是可以的
向量的范数就是把向量变成一个标量,范数的表示就是两个竖线来表示,然后右下角写上 P
$$||x||p = (\sum{i=1}^{n}|x_i|^p)^\frac{1}{p}$$
1 范数是绝对值加和,1 范数写成 L1
$$
||x||1 = \sum{i=1}^{n}|x_i|
$$
2 范数是平方加和开根号,其实代表的是向量的长度,高中时候学的向量的模,2 范数写成 L2
$$
||x||2 = \sqrt{\sum{i=1}^{n}(x_i)^2}
$$
范数在后面是非常有用的,在后面讲正则项的时候会用到
L1范数的正则项:$$\sum_{i=1}^{n}|w_i|$$
L2范数的正则项:$$\sum_{i=1}^{n}(w_i)^2$$
几何意义
赫尔曼·闵可夫斯基在少年时期就在数学方面表现出极高的天分,他是后来四维时空理论的创立者,也曾经是著名物理学家爱因斯坦的老师。
曼哈顿距离也叫出租车距离,用来标明两个点在标准坐标系上的绝对轴距总和。简单来说,对比一下欧氏距离。
欧氏距离里的距离计算:
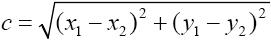
曼哈顿距离中的距离计算:
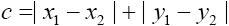
曼哈顿距离中的距离计算公式比欧氏距离的计算公式看起来简洁很多,只需要把两个点坐标的 x 坐标相减取绝对值,y 坐标相减取绝对值,再加和。
从公式定义上看,曼哈顿距离一定是一个非负数,距离最小的情况就是两个点重合,距离为 0,这一点和欧氏距离一样。曼哈顿距离和欧氏距离的意义相近,也是为了描述两个点之间的距离,不同的是曼哈顿距离只需要做加减法,这使得计算机在大量的计算过程中代价更低,而且会消除在开平方过程中取近似值而带来的误差。不仅如此,曼哈顿距离在人脱离计算机做计算的时候也会很方便。举例如下。

在国际象棋棋盘(图 2)上,有这种横平竖直的格子,描述格子和格子之间的距离可以直接用曼哈顿距离。如 A1 格子到 C4 格子的曼哈顿距离计算如下:
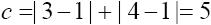
两个格子之间的曼哈顿距离为 5。
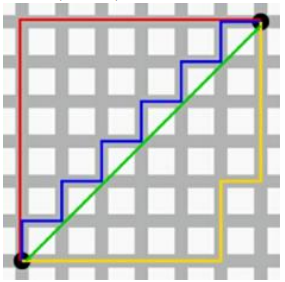
之所以曼哈顿距离又被称为出租车距离是因为在像纽约曼哈顿区这样的地区有很多由横平竖直的街道所切成的街区(Block),出租车司机计算从一个位置到另一个位置的距离,通常直接用街区的两个坐标分别相减,再相加,这个结果就是他即将开车通过的街区数量,而完全没有必要用欧氏距离来求解——算起来超级麻烦还没有意义,毕竟谁也没办法从欧氏距离的直线上飞过去。如图 3 所示,假设一辆出租车要从上面的圆圈位置走到下面的圆圈位置,无论是左边的线路,还是右边的线路,都要经过 11 个街区,而这个 11 就是曼哈顿距离。
从曼哈顿距离的定义就能看出,曼哈顿距离的创立,与其说有很大的学术意义不如说更多的是应用意义。这也是本书一直想说的一点,数学就在我们身边,它是我们的工具,能帮我们解决问题而不是带来麻烦。

上面的公式只给了二维空间上的曼哈顿距离公式,三维、四维或者更多维度的计算原理是一样
