Greedy-NAS用到了这个算法,看了2天才整明白,所以来总结一下:
以下为源码的链接,下载需要软妹币哦:
一.原理讲解:
Pareto支配(Pareto Dominate)
Pareto支配在MOP问题中支配是一个重要的概念,以下简称为支配。
支配的描述为:有两个解x1和x2,x1支配x2的充要条件是对于任意的i(i=1,2, 3...m),均有fi(x1)<=fi(x2),且对于任意的i(i=1, 2, 3...m),存在fi(x1)<fi(x2)。记为x1≺x2。(和离散数学里的偏序关系相似)
这个概念看起来不好懂?其实就类似于小于关系,我的记法很简单:全部小于等于,至少1个小于。
Pareto最优解(Pareto Optimal Solution)
某个解x'是最优解,当且仅当x'不被任何其他解支配。
大家是否发现,x'只是不被其他解支配,而不是支配了其他所有解,就能称为最优解了。前面说过,MOP问题往往求出很多个解,这些解的优劣关系是无法确定的。
只要某个解不被其他解支配,就说明这个解不比其他解差,就能称其为最优解了。
Pareto集(Pareto Set)
如果一组解集(也就是多个x)中的任意两个解都不能支配对方,那么这个集合称为Pareto集,简称PS。
Pareto前沿(Pareto Front)
PS中,每个解对应的目标函数值组成的集合称为pareto前沿,简称PF。
进化算法是如何解决MOP问题的呢?
主要是3个应用:变异、交叉、多样性。
-
变异
我就直接解释了:取某一个解x0,让x0随机地变化,比如增加0.1得x1,减少0.1得x2之类,看看变化之后和原来有什么不同。
要是变化之后,发现了更左下的点?是不是就说明发现了更优的解?这时我们可以保留左下的点、淘汰右上的点。这是不是和生物的变异、优胜劣汰非常相似?
需要注意的是:变异不是一定能够产生更左下的点的,但是只要出现了,我们就能把它保留下来!
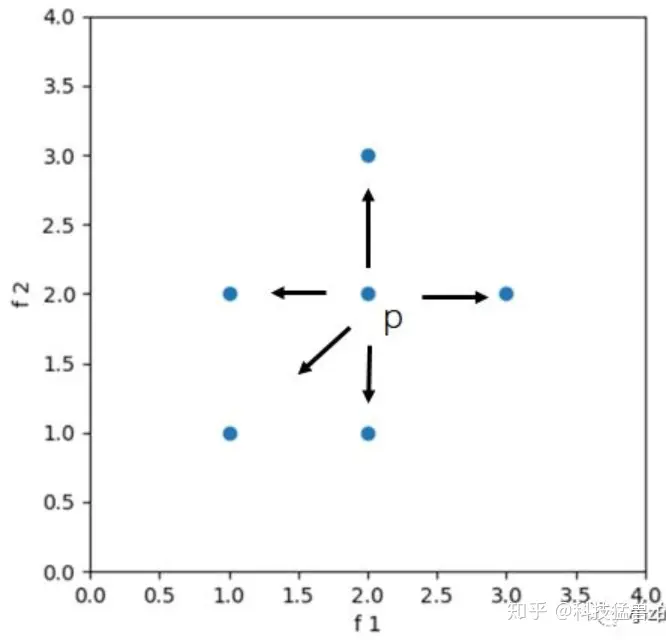
如图,p点可以变异形成另外四个点,我们可以保留更左下的点。
-
交叉
叫做交配更好理解。直接上解释:假如有两个解x1和x2,分别对应左上的p1和右下的p2,那么我们可以想办法融合x1和x2的优良性状,这就是交叉。
比如,我们可以取x3=(x1+x2)/2,看看x3相对于x1和x2的位置,要是x3是更优的解,同样可以保留x3。
和变异相同,交叉也不是一定能产生更左下的点的。 -
多样性
多样性这个概念不是很好理解,这里再次祭出真实的求解结果。
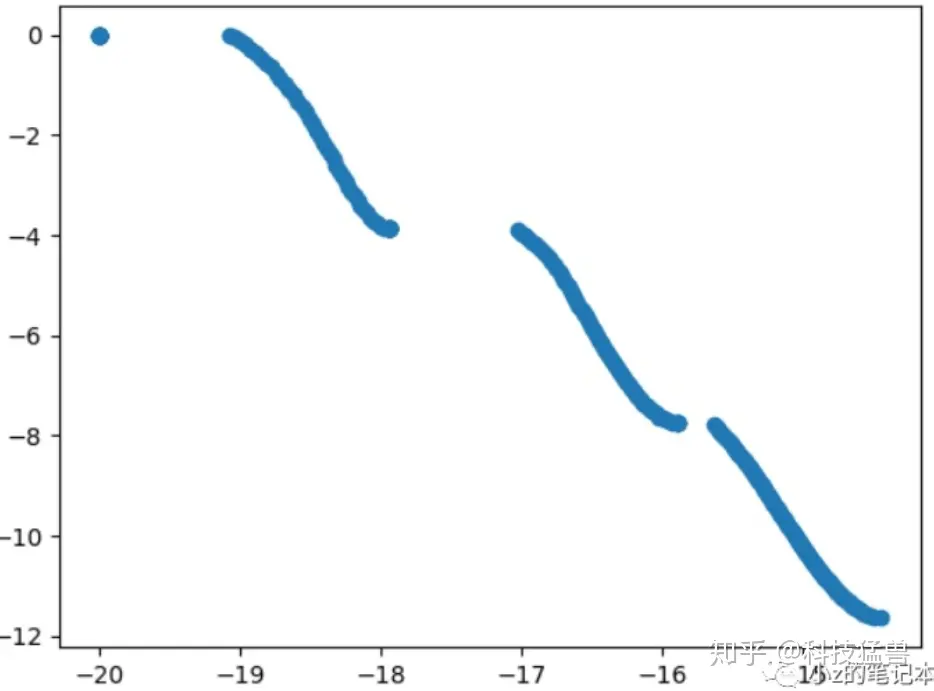
忽略最左边的点,可以发现有三条线。
所谓多样性就是:保持 找到尽可能多的解的 可能性。从上往下,分别为种群1,2,3。
在变异和交叉里我们提到了淘汰和保留。要是稍微往右或者往上的点都被淘汰了,留下的全是往左下的点,就可能导致最后只发展成了种群2,种群1和3都没有出现!因为有可能发展出种群1和3的个体因为过于严格的选择方法,早早就被淘汰掉了,根本没有发展的机会。
可见,如何淘汰和保留也是有技巧的。
-
总能找到最优解
进化算法的思想虽然有点非主流,但是给它足够的时间,它总是能让你得到满意的结果!
进化算法的步骤就是:
任意初始化一个种群,一个种群就是很多个个体的集合,1个个体就是1个解(一开始我还不理解真的是任意吗?后来去看了算法的源代码发现还真是用的任意数!可能也保证了种群的多样性)。
让这些个体变异、交叉(随机地变化、相互结合产生新的解),然后看保留优良的个体(往左下的点),同时要保持种群多样性,以保留发展出新种群的可能性(让右下和左上的点也有几率留下来)。
经过若干代,种群就会趋于稳定(解已经很接近真实的最优解了)。进化到一定次数就停止算法。
NSGA-Ⅱ算法
既然有Ⅱ自然是有Ⅰ的,这里不说Ⅰ,只说Ⅱ。为什么不说Ⅰ,很简单,因为我不会。
MSGA-Ⅱ的思想也是进化算法的思想。你如果懂了进化算法的思想,也会很容易懂NSGA-Ⅱ。
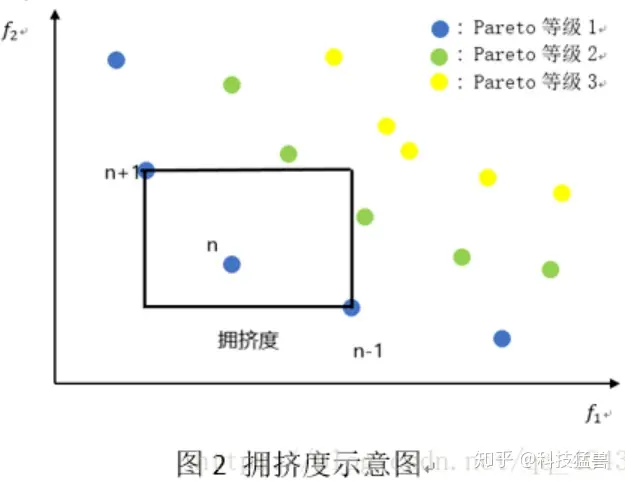
NSGA-Ⅱ中还包含了一个选择个体的方法:拥挤度比较
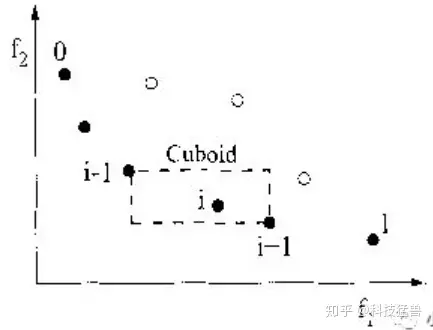
i的拥挤度和i-1点和i+1点的位置有关,上图i点的拥挤度就是方形的周长(也就是虚线的总长度)。最左边和最右边的点的拥挤度设置为无限大。
我们喜欢拥挤度大的点(拥挤度大实际上是和周围的点相隔远),因为它们更能保持种群多样性,更容易发展出新种群。
前面说了,左上和右下的点是无法比较的,但是拥挤度提供了一个比较的思路。
下面举一个简单的例子演示NSGA-Ⅱ算法的流程。设种群大小为5,目标函数2个,f1和f2我想不到合适的,就不管了。
-
初始化
初始化5个个体为初代。
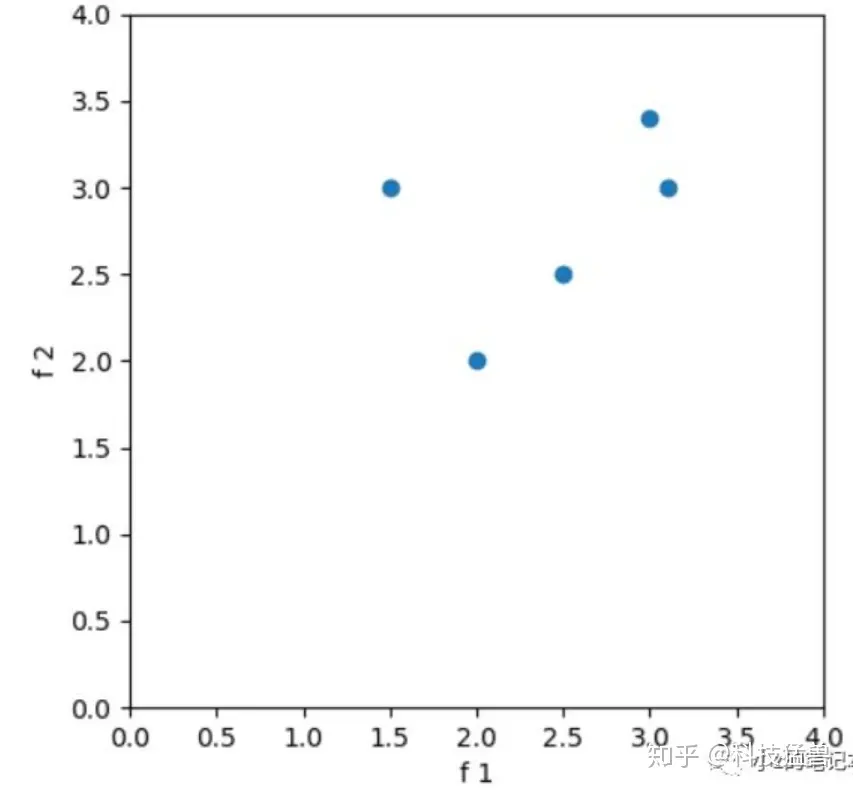
-
交叉、变异
原先的5个个体变异,再任选两个进行交叉,交叉又产生5个个体,现在总共有10个个体了。 -
非支配排序
把种群分成几个PS并赋予等级,越往左下的PS等级越高(因为越优)。rank越小,等级越高。
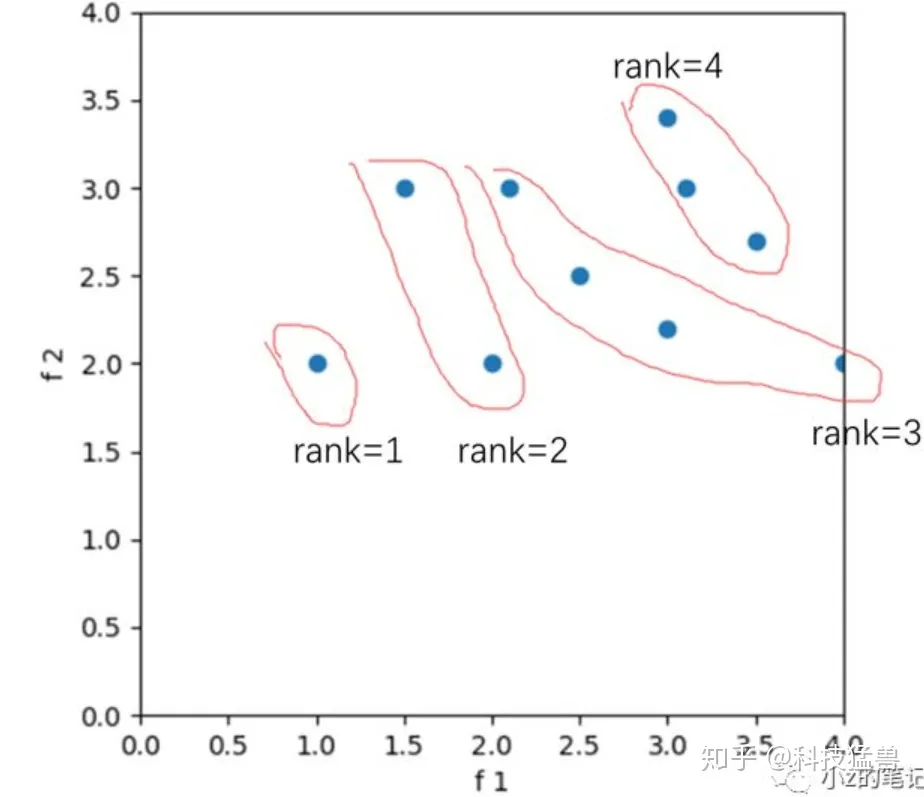
-
选择
我们自然是选择rank高的个体了,rank=1和rank=2的个体,总共3个被保留。
我们要再次凑成5个个体的种群。我们就在rank=3的个体中选,但是也不能全要,因为会超过5个!
那咋办嘛?这就用到拥挤度了,选择拥挤度大的,那么就是最左边和最右边的两个,因为我们定义了这两个的拥挤度是无限大。 -
迭代
选择完了又回到第2步,直到进化到了一定的次数,结束算法。
二.具体方法论:
1.1 Pareto支配关系以及Pareto等级

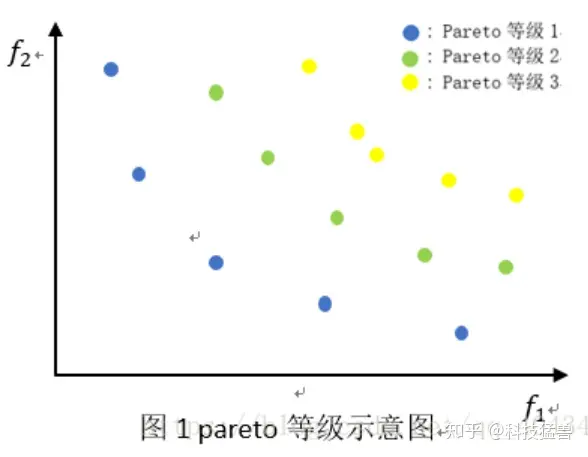
1.2 快速非支配排序

1.3 拥挤度

1.4 精英保留策略

1.5 实数编码的交叉操作(SBX)
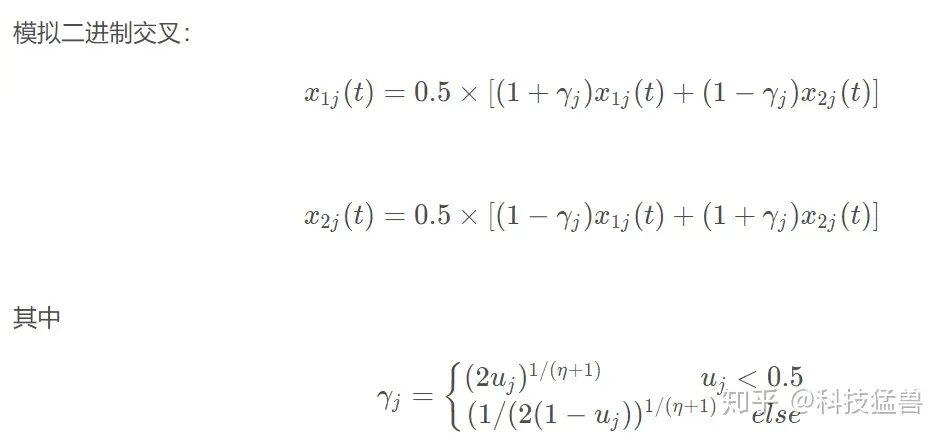
1.6 多项式变异(polynomial mutation)
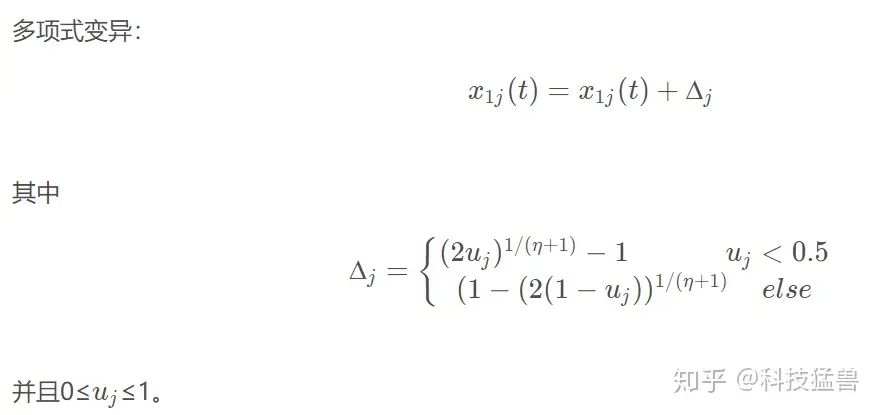
1.7 竞标赛选择(tournament selection)

2. 算法实现框图

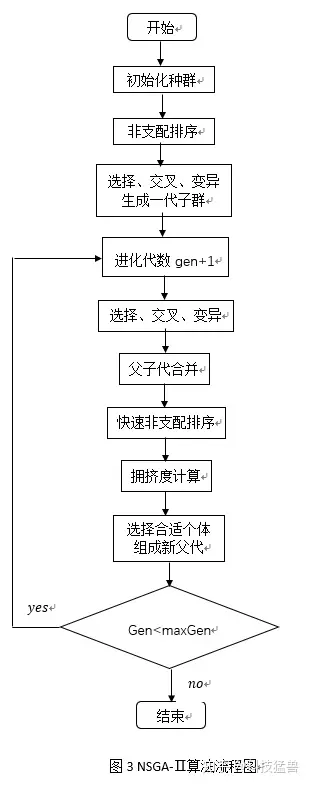
三.代码:
首先贴出主函数代码,对应整个流程图:
function nsga_2_optimization
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%此处可以更改
%更多机器学习内容请访问omegaxyz.com
pop = 200; %种群数量
gen = 500; %迭代次数
M = 2; %目标函数数量
V = 30; %维度(决策变量的个数)
min_range = zeros(1, V); %下界 生成1*30的个体向量 全为0
max_range = ones(1,V); %上界 生成1*30的个体向量 全为1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
chromosome = initialize_variables(pop, M, V, min_range, max_range);%初始化种群
chromosome = non_domination_sort_mod(chromosome, M, V);%对初始化种群进行非支配快速排序和拥挤度计算
for i = 1 : gen
pool = round(pop/2);%round() 四舍五入取整 交配池大小
tour = 2;%竞标赛 参赛选手个数
parent_chromosome = tournament_selection(chromosome, pool, tour);%竞标赛选择适合繁殖的父代
mu = 20;%交叉和变异算法的分布指数
mum = 20;
offspring_chromosome = genetic_operator(parent_chromosome,M, V, mu, mum, min_range, max_range);%进行交叉变异产生子代 该代码中使用模拟二进制交叉和多项式变异 采用实数编码
[main_pop,~] = size(chromosome);%父代种群的大小
[offspring_pop,~] = size(offspring_chromosome);%子代种群的大小
clear temp
intermediate_chromosome(1:main_pop,:) = chromosome;
intermediate_chromosome(main_pop + 1 : main_pop + offspring_pop,1 : M+V) = offspring_chromosome;%合并父代种群和子代种群
intermediate_chromosome = non_domination_sort_mod(intermediate_chromosome, M, V);%对新的种群进行快速非支配排序
chromosome = replace_chromosome(intermediate_chromosome, M, V, pop);%选择合并种群中前N个优先的个体组成新种群
if ~mod(i,100)
clc;
fprintf('%d generations completed\n',i);
end
end
if M == 2
plot(chromosome(:,V + 1),chromosome(:,V + 2),'*');
xlabel('f_1'); ylabel('f_2');
title('Pareto Optimal Front');
elseif M == 3
plot3(chromosome(:,V + 1),chromosome(:,V + 2),chromosome(:,V + 3),'*');
xlabel('f_1'); ylabel('f_2'); zlabel('f_3');
title('Pareto Optimal Surface');
end1 初始化代码
对于f(i)来说,前V个元素为决策变量,V+1到V+M个元素为M个目标函数的值,第V+M+1个元素为pareto等级。第V+M+2个元素为拥挤度。决策变量就是相当于DNA一样,用于杂交和变异。
function f = initialize_variables(N, M, V, min_range, max_range)%f是一个由种群个体组成的矩阵
min = min_range;
max = max_range;
K = M + V;%%K是数组的总元素个数。为了便于计算,决策变量和目标函数串在一起形成一个数组。
%对于交叉和变异,利用目标变量对决策变量进行选择
for i = 1 : N
for j = 1 : V
f(i,j) = min(j) + (max(j) - min(j))*rand(1);%f(i j)表示的是种群中第i个个体中的第j个决策变量,
%这行代码为每个个体的所有决策变量在约束条件内随机取值
end
f(i,V + 1: K) = evaluate_objective(f(i,:), M, V); % M是目标函数数量 V是决策变量个数
%为了简化计算将对应的目标函数值储存在染色体的V + 1 到 K的位置。
end2 快速非支配排序和拥挤度计算代码
individual(i).n是能支配个体i的个体数量。
individual(i).p =[]是被个体i支配的个体集合。
sorted_based_on_front中存放的是x矩阵按照排序等级升序排序后的矩阵。
y中存放的是排序等级为front的集合矩阵。
sorted_based_on_objective存放按照目标函数值排序后的x矩阵。
返回每个个体对应的Rank值和拥挤距离,是一个两列的矩阵。
%% 对初始种群开始排序 快速非支配排序
% 使用非支配排序对种群进行排序。该函数返回每个个体对应的排序值和拥挤距离,是一个两列的矩阵。
% 并将排序值和拥挤距离添加到染色体矩阵中
function f = non_domination_sort_mod(x, M, V)
[N, ~] = size(x);% N为矩阵x的行数,也是种群的数量
clear m
front = 1;
F(front).f = [];
individual = [];
for i = 1 : N
individual(i).n = 0;%n是个体i被支配的个体数量
individual(i).p = [];%p是被个体i支配的个体集合
for j = 1 : N
dom_less = 0;
dom_equal = 0;
dom_more = 0;
for k = 1 : M %判断个体i和个体j的支配关系
if (x(i,V + k) < x(j,V + k))
dom_less = dom_less + 1;
elseif (x(i,V + k) == x(j,V + k))
dom_equal = dom_equal + 1;
else
dom_more = dom_more + 1;
end
end
if dom_less == 0 && dom_equal ~= M % 说明i受j支配,相应的n加1
individual(i).n = individual(i).n + 1;
elseif dom_more == 0 && dom_equal ~= M % 说明i支配j,把j加入i的支配合集中
individual(i).p = [individual(i).p j];
end
end
if individual(i).n == 0 %个体i非支配等级排序最高,属于当前最优解集,相应的染色体中携带代表排序数的信息
x(i,M + V + 1) = 1;
F(front).f = [F(front).f i];%等级为1的非支配解集
end
end
%上面的代码是为了找出等级最高的非支配解集
%下面的代码是为了给其他个体进行分级
while ~isempty(F(front).f)
Q = []; %存放下一个front集合
for i = 1 : length(F(front).f)%循环当前支配解集中的个体
if ~isempty(individual(F(front).f(i)).p)%个体i有自己所支配的解集
for j = 1 : length(individual(F(front).f(i)).p)%循环个体i所支配解集中的个体
individual(individual(F(front).f(i)).p(j)).n = ...%...表示的是与下一行代码是相连的, 这里表示个体j的被支配个数减1
individual(individual(F(front).f(i)).p(j)).n - 1;
if individual(individual(F(front).f(i)).p(j)).n == 0% 如果q是非支配解集,则放入集合Q中
x(individual(F(front).f(i)).p(j),M + V + 1) = ...%个体染色体中加入分级信息
front + 1;
Q = [Q individual(F(front).f(i)).p(j)];
end
end
end
end
front = front + 1;
F(front).f = Q;
end
[temp,index_of_fronts] = sort(x(:,M + V + 1));%对个体的代表排序等级的列向量进行升序排序 index_of_fronts表示排序后的值对应原来的索引
for i = 1 : length(index_of_fronts)
sorted_based_on_front(i,:) = x(index_of_fronts(i),:);%sorted_based_on_front中存放的是x矩阵按照排序等级升序排序后的矩阵
end
current_index = 0;
%% Crowding distance 计算每个个体的拥挤度
for front = 1 : (length(F) - 1)%这里减1是因为代码55行这里,F的最后一个元素为空,这样才能跳出循环。所以一共有length-1个排序等级
distance = 0;
y = [];
previous_index = current_index + 1;
for i = 1 : length(F(front).f)
y(i,:) = sorted_based_on_front(current_index + i,:);%y中存放的是排序等级为front的集合矩阵
end
current_index = current_index + i;%current_index =i
sorted_based_on_objective = [];%存放基于拥挤距离排序的矩阵
for i = 1 : M
[sorted_based_on_objective, index_of_objectives] = ...
sort(y(:,V + i));%按照目标函数值排序
sorted_based_on_objective = [];
for j = 1 : length(index_of_objectives)
sorted_based_on_objective(j,:) = y(index_of_objectives(j),:);% sorted_based_on_objective存放按照目标函数值排序后的x矩阵
end
f_max = ...
sorted_based_on_objective(length(index_of_objectives), V + i);%fmax为目标函数最大值 fmin为目标函数最小值
f_min = sorted_based_on_objective(1, V + i);
y(index_of_objectives(length(index_of_objectives)),M + V + 1 + i)...%对排序后的第一个个体和最后一个个体的距离设为无穷大
= Inf;
y(index_of_objectives(1),M + V + 1 + i) = Inf;
for j = 2 : length(index_of_objectives) - 1%循环集合中除了第一个和最后一个的个体
next_obj = sorted_based_on_objective(j + 1,V + i);
previous_obj = sorted_based_on_objective(j - 1,V + i);
if (f_max - f_min == 0)
y(index_of_objectives(j),M + V + 1 + i) = Inf;
else
y(index_of_objectives(j),M + V + 1 + i) = ...
(next_obj - previous_obj)/(f_max - f_min);
end
end
end
distance = [];
distance(:,1) = zeros(length(F(front).f),1);
for i = 1 : M
distance(:,1) = distance(:,1) + y(:,M + V + 1 + i);
end
y(:,M + V + 2) = distance;
y = y(:,1 : M + V + 2);
z(previous_index:current_index,:) = y;
end
f = z();%得到的是已经包含等级和拥挤度的种群矩阵 并且已经按等级排序排序
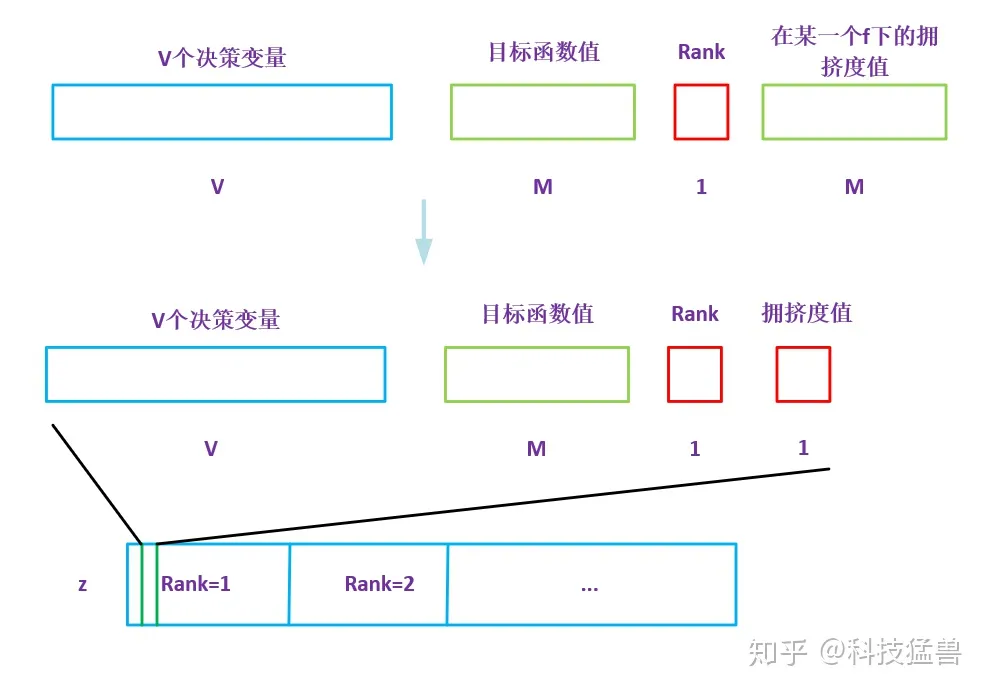
3 竞标赛选择代码
pool = round(pop/2):交配池大小
tour = 2:竞标赛 参赛选手个数
从pop个里面竞标出pop/2个牛逼一点的。
chromosome是一个矩阵,行数是pop的个数,列数是(V+M+2=决策变量数+目标函数维数+等级+拥挤度)。
function f = tournament_selection(chromosome, pool_size, tour_size)
[pop, variables] = size(chromosome);%获得种群的个体数量和决策变量数量
rank = variables - 1;%个体向量中排序值所在位置
distance = variables;%个体向量中拥挤度所在位置
%竞标赛选择法,每次随机选择两个个体,优先选择排序等级高的个体,如果排序等级一样,优选选择拥挤度大的个体
for i = 1 : pool_size
for j = 1 : tour_size
candidate(j) = round(pop*rand(1));%随机选择参赛个体
if candidate(j) == 0
candidate(j) = 1;
end
if j > 1
while ~isempty(find(candidate(1 : j - 1) == candidate(j)))%防止两个参赛个体是同一个
candidate(j) = round(pop*rand(1));
if candidate(j) == 0
candidate(j) = 1;
end
end
end
end
for j = 1 : tour_size% 记录每个参赛者的排序等级 拥挤度
c_obj_rank(j) = chromosome(candidate(j),rank);
c_obj_distance(j) = chromosome(candidate(j),distance);
end
min_candidate = ...
find(c_obj_rank == min(c_obj_rank));%选择排序等级较小的参赛者,find返回该参赛者的索引
if length(min_candidate) ~= 1%如果两个参赛者的排序等级相等 则继续比较拥挤度 优先选择拥挤度大的个体
max_candidate = ...
find(c_obj_distance(min_candidate) == max(c_obj_distance(min_candidate)));
if length(max_candidate) ~= 1
max_candidate = max_candidate(1);
end
f(i,:) = chromosome(candidate(min_candidate(max_candidate)),:);
else
f(i,:) = chromosome(candidate(min_candidate(1)),:);
end
end4、5 交叉 变异代码
把这pop/2个牛逼的 杂交变异 得到pop个子代。
这里面N=pop/2,交叉的双亲分别是parent_1和parent_2。
child_1(j)是30维的。
function f = genetic_operator(parent_chromosome, M, V, mu, mum, l_limit, u_limit)
[N,m] = size(parent_chromosome);%N是交配池中的个体数量
clear m
p = 1;
was_crossover = 0;%是否交叉标志位
was_mutation = 0;%是否变异标志位
for i = 1 : N%这里虽然循环N次,但是每次循环都会有概率产生2个或者1个子代,所以最终产生的子代个体数量大约是2N个
if rand(1) < 0.9%交叉概率0.9
child_1 = [];
child_2 = [];
parent_1 = round(N*rand(1));
if parent_1 < 1
parent_1 = 1;
end
parent_2 = round(N*rand(1));
if parent_2 < 1
parent_2 = 1;
end
while isequal(parent_chromosome(parent_1,:),parent_chromosome(parent_2,:))
parent_2 = round(N*rand(1));
if parent_2 < 1
parent_2 = 1;
end
end
parent_1 = parent_chromosome(parent_1,:);
parent_2 = parent_chromosome(parent_2,:);
for j = 1 : V
u(j) = rand(1);
if u(j) <= 0.5
bq(j) = (2*u(j))^(1/(mu+1));
else
bq(j) = (1/(2*(1 - u(j))))^(1/(mu+1));
end
child_1(j) = ...
0.5*(((1 + bq(j))*parent_1(j)) + (1 - bq(j))*parent_2(j));
child_2(j) = ...
0.5*(((1 - bq(j))*parent_1(j)) + (1 + bq(j))*parent_2(j));
if child_1(j) > u_limit(j)
child_1(j) = u_limit(j);
elseif child_1(j) < l_limit(j)
child_1(j) = l_limit(j);
end
if child_2(j) > u_limit(j)
child_2(j) = u_limit(j);
elseif child_2(j) < l_limit(j)
child_2(j) = l_limit(j);
end
end
child_1(:,V + 1: M + V) = evaluate_objective(child_1, M, V);
child_2(:,V + 1: M + V) = evaluate_objective(child_2, M, V);
was_crossover = 1;
was_mutation = 0;
else%if >0.9
parent_3 = round(N*rand(1));
if parent_3 < 1
parent_3 = 1;
end
child_3 = parent_chromosome(parent_3,:);
for j = 1 : V
r(j) = rand(1);
if r(j) < 0.5
delta(j) = (2*r(j))^(1/(mum+1)) - 1;
else
delta(j) = 1 - (2*(1 - r(j)))^(1/(mum+1));
end
child_3(j) = child_3(j) + delta(j);
if child_3(j) > u_limit(j) % 条件约束
child_3(j) = u_limit(j);
elseif child_3(j) < l_limit(j)
child_3(j) = l_limit(j);
end
end
child_3(:,V + 1: M + V) = evaluate_objective(child_3, M, V);
was_mutation = 1;
was_crossover = 0;
end% if <0.9
if was_crossover
child(p,:) = child_1;
child(p+1,:) = child_2;
was_cossover = 0;
p = p + 2;
elseif was_mutation
child(p,:) = child_3(1,1 : M + V);
was_mutation = 0;
p = p + 1;
end
end
f = child;交叉算法选择的是模拟二进制交叉,变异算法选择的是多项式变异,上面的原理部分有讲到,如下图所示:
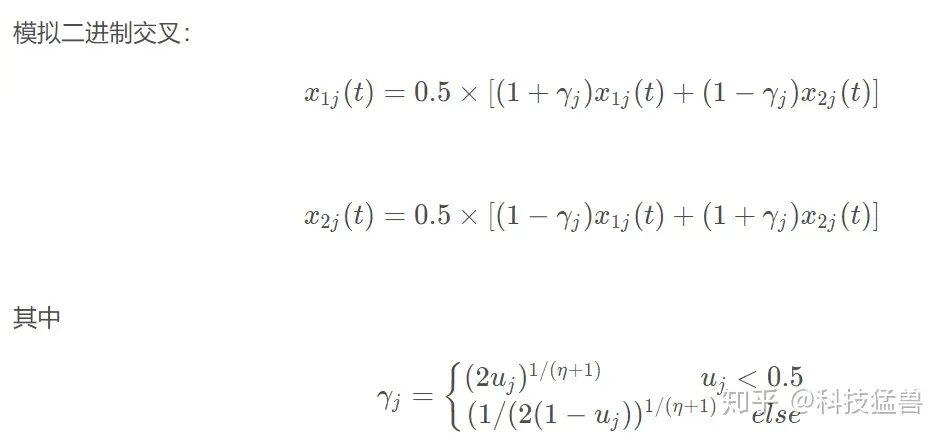
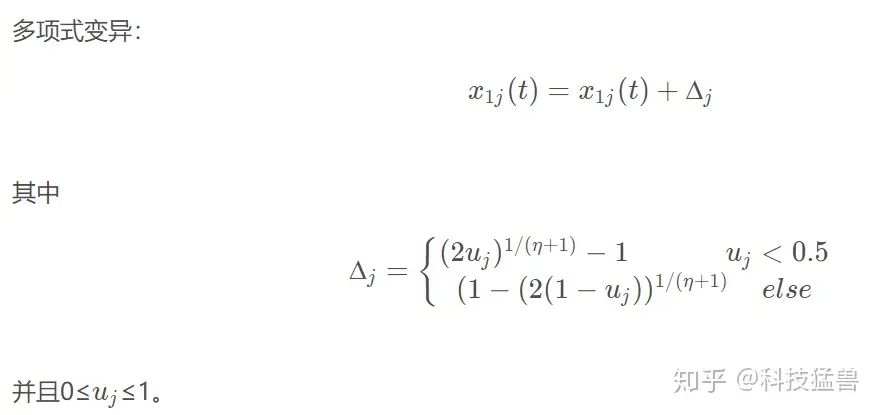
8 生成新的种群(精英策略)
sorted_chromosome就是排完顺序的intermediate_chromosome。
function f = replace_chromosome(intermediate_chromosome, M, V,pop)%精英选择策略
[N, m] = size(intermediate_chromosome);
[temp,index] = sort(intermediate_chromosome(:,M + V + 1));
clear temp m
for i = 1 : N
sorted_chromosome(i,:) = intermediate_chromosome(index(i),:);
end
max_rank = max(intermediate_chromosome(:,M + V + 1));
previous_index = 0;
for i = 1 : max_rank
current_index = max(find(sorted_chromosome(:,M + V + 1) == i));
if current_index > pop
remaining = pop - previous_index;
temp_pop = ...
sorted_chromosome(previous_index + 1 : current_index, :);
[temp_sort,temp_sort_index] = ...
sort(temp_pop(:, M + V + 2),'descend');
for j = 1 : remaining
f(previous_index + j,:) = temp_pop(temp_sort_index(j),:);
end
return;
elseif current_index < pop
f(previous_index + 1 : current_index, :) = ...
sorted_chromosome(previous_index + 1 : current_index, :);
else
f(previous_index + 1 : current_index, :) = ...
sorted_chromosome(previous_index + 1 : current_index, :);
return;
end
previous_index = current_index;
end本例子选择的测试函数是ZDT1, 目标评价函数如下:
function f = evaluate_objective(x, M, V)%%计算每个个体的M个目标函数值
f = [];
f(1) = x(1);
g = 1;
sum = 0;
for i = 2:V
sum = sum + x(i);
end
sum = 9*(sum / (V-1));
g = g + sum;
f(2) = g * (1 - sqrt(x(1) / g));
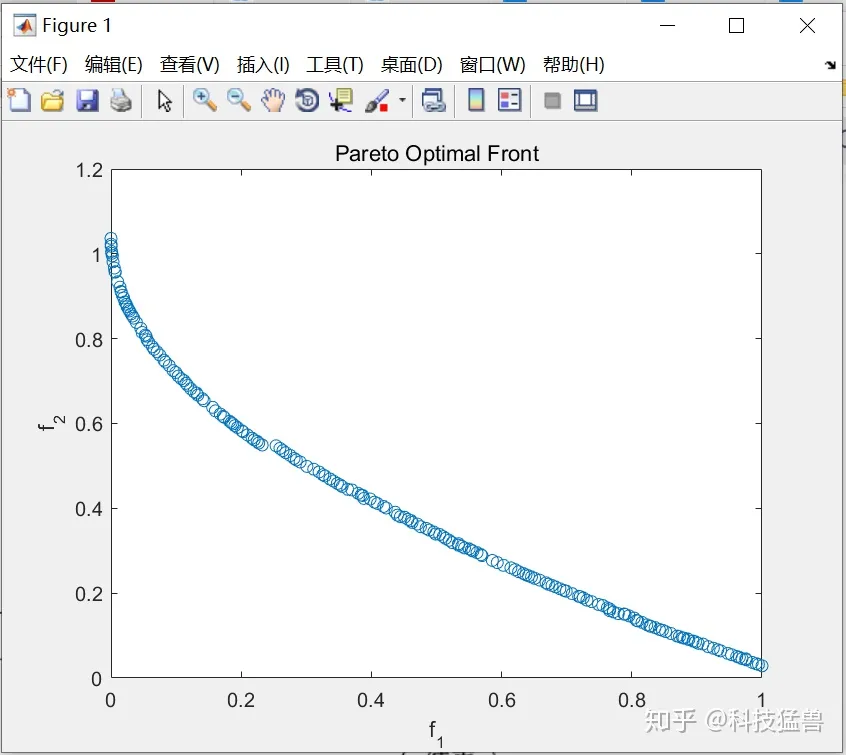
end经历500次迭代后的pareto最优解集:
原理部分参考了以下这篇文章:

