序言
- 区分一下这几个概念
1. 点乘
- 点乘 = 点积 = 内积 = 数量积
- dot product = inner product = scalar product
-
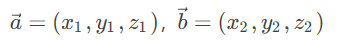
- 从代数角度看，点积是对两个向量对应位置上的值相乘再相加的操作，其结果即为点积
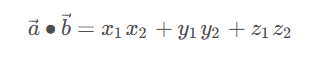
- 点乘的几何意义：向量b在向量a方向上的投影与向量a的模的乘积，用来表征或计算两个向量间的夹角，表征两个向量在方向上的相似度，结果越大越相似
-
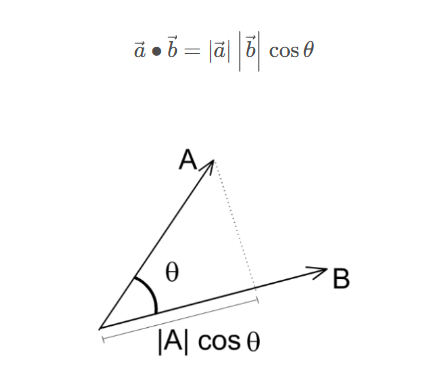
基于点乘结果可以判断这两个向量是否是同一方向，是否正交垂直，具体对应关系：
点乘 > 0：向量夹角在0~90°之间 点乘 = 0：正交，相互垂直 点乘 -
公式推导
1. 向量c = a - b 2. c^2 = a^2 + b^2 - 2abcos(theta) 3. (a - b) ▪ (a - b) = a^2 + b^2 – 2a▪b = a^2 + b^2 - 2abcos(theta)
2. 叉乘
-
叉乘 = 叉积 = 外积 = 向量积
-
cross product = outer product
-
-
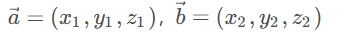
从代数角度计算：
-
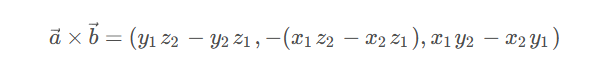
从几何角度计算
- 其中
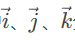分别是x轴、y轴、z轴方向的单位向量 - 当
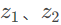等于0的时候，即得到二维向量叉乘的结果
- 其中
-
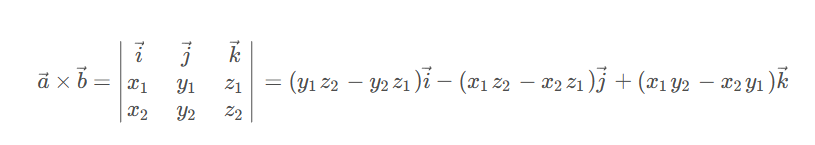
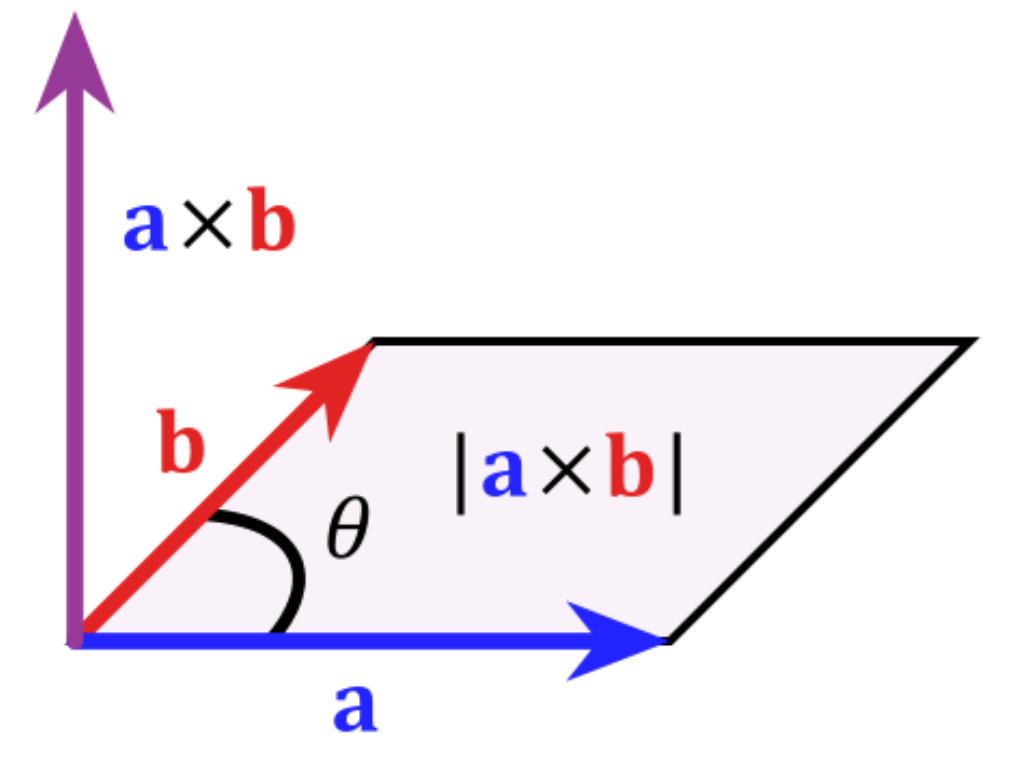
叉乘的几何意义：
- 二维向量叉乘：向量a和向量b的叉乘表示向量a和b构成的平行四边形的面积
- 二维向量叉乘：如果a或b其中一个为单位向量，则axb叉乘结果表示以单位向量为底的平行四边形的高，可以有正负
- 三维向量叉乘：向量a和向量b的叉乘结果是一个向量，该向量垂直于向量a和b组成的平面，即平面的法向量，方向遵守右手定则
-
叉积有一个非常重要的性质，可通过叉积的符号来判断两向量的顺逆时针关系
P x Q > 0, 则向量P在向量Q的顺时针方向； P x Q
3. 点乘 vs 叉乘，对比与应用
- 点乘的结果是标量(常用于物理)/数量(常用于数学)，可以用来计算夹角和投影
- 叉乘的结果是矢量(常用于物理)/向量(常用于数学)，法向量的模大小为
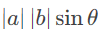，方向遵守右手定则 - 在二维空间中，叉乘结果等于向量a和b构成的平行四边形的面积，平行四边形的面积：以
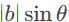为高，以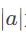
为底。当a是单位向量时，计算b的终点到a所在直线的距离，也就是平行四边形的高
- 通过向量的叉乘生成垂直于向量a/b的法向量，从而构建XYZ坐标系
- 叉乘的结果再点乘可以用来判断向量/线段是否相交，即"跨立实验"，见文章判断两条线段是否相交